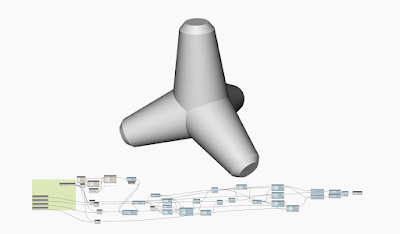
Recently I’ve been asked about how to make a Tetra-Pod with Dynamo. After I created one, I felt it’s a quite simple but good example of using geometrical construction in Dynamo, so I’m posting about it.
Basically, the geometry of a Tetra-Pod is from a regular tetrahedron as it’s name. So if a regular tetrahedron could be created, making a Tetra-Pod would be not very difficult.
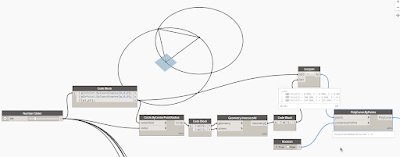
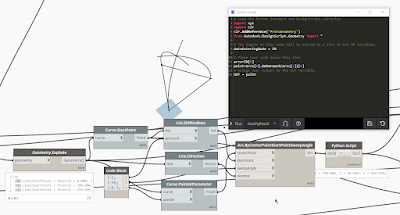
Actually, I’ve already posted about creating five kinds of regular polyhedrons. I used math to find each necessary angles then. This time, I didn’t use any math calculations to find angles. I used pure geometrical methods instead. Geometrical constructions are useful especially when you want to avoid errors of float numbers.
1. Define regular triangle for bottom (in geometrical method)
RegularPolygon node can be used for creating a regular triangle, but I got one by geometrical method which is just like using a compass on a drafting board.